he global coordinate system (Z, Y) and (b) the local coordinate system (x,j^). Reproduced from Ogawa et al. 2006 with permission
Model of the Torque
The phenomenon whereby a Paramecium cell swims toward the cathode is due to a torque caused by asymmetry of ciliary motion. In this section, we estimate this torque. Note that the following model is defined only if £' ^ 0. First, consider an ellipsoid S" in the local coordinate system {x,y), as il-lustrated in Fig. 2(b). In the substantially trapezoidal region formed by the intersection of the boundary plane and the ellipsoid shown as the hatched region in Fig. 2(b), beating direction of cilia on both sides differ, thus caus-ing asymmetry in forces. The forces generated by the cilia on the cell other than the region do not contribute to the torque generation. Thus, we have only to consider the forces generated at this hatched region. For convenience, let us introduce 0 = —0 as the angle of the electric field E in the local coordinate system. Because it would be too complicated to consider the individual minute forces generated by each cilium, here we focus on the resultant forces for simplicity. We set sites of action, Pi(xa,ya) and P2(^a,->^a)? at the mid-points of the sides of the trapezoid and assume the directions of the forces to be tangential to the ellipsoid. We then define position vectors, ri = OPi and r2 = OP2. Next, let us suppose that the magnitude of the resultant force is proportional to the "height" of the trapezoid w, which is a signed value of the same sign as 6. Then, the propelling forces Fi and F2 at the points Pi and P2, respectively, are represented by /^{i,2} = Tf^n^{\,2}, where m\ and 1W2 are the unit tangent vectors at Pi and P2, and the =F symbol indi-cates the two directions of ciliary beating. Thus, we find the torques at the points P{i,2}5 namely, T{i 2} = ^{1,2} x ^{1,2}• It should be noted that these
vectors are treated as three-dimensional in calculating cross products. The total torque rotating the cell body is given by T = Ti + T2- Since its x and y components are obviously zero, hereafter we call its z component, T^, the "torque". Finally, by substituting 0 = —9, the torque is described in the global coordinate system as:
where 5* = sin0 and c = cos 0. This equation describes the torque generated in a cell oriented at angle 0.

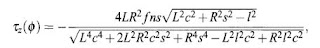

No comments:
Post a Comment