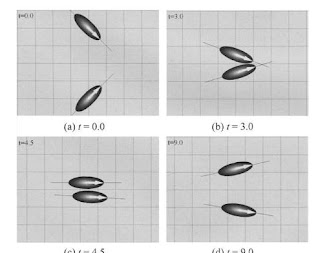
Sequences (a) to (d) showing the hydrodynamic interactions between two squirmers, where / is the dimensionless time. The orientation vectors of the squirmers are shown as large arrows on the ellipsoids, and a thin solid line is added so that one can easily compare the angle between the two squirmers. (Ishi-kawa and Hota

 practice is unlikely to exist.) The present results show, however, that the near-field interaction dramatically changes the orientation of cells. Since orientation change affects the macroscopic properties of the suspension, such as the diffusivity, the near-field interaction has to be solved accu-rately

 A semi-dilute suspension of squirmers

 Methods 

 23 practice is unlikely to exist.) The present results show, however, that the near-field interaction dramatically changes the orientation of cells. Since orientation change affects the macroscopic properties of the suspension, such as the diffusivity, the near-field interaction has to be solved accu-rately. 3 A semi-dilute suspension of squirmers 3.1 Methods In the following secfions, a squirmer is assumed to have a spherical shape for simplicity. The surface velocities of a squirmer model was analyzed by Blake (1971), and we use a simplified version of his equation given by; ''S=T——^B\ elp;, (3) where e is the orientation vector, r is the position vector and r = |r|. P^ is the nth Legendre polynomial, and B^ is the nth mode of the surface squirm-ing velocity, (see details in Ishikawa etal, 2006) A sample squirmer, which will be used in the following sections, gen-erates velocity vectors, relative to a frame of reference in which the squirmer's centre is at rest, as shown in figure 4. The orientation vector of the squirmer is also shown, and the uniform flow of its swimming speed comes from the far right. The numerical method for a semi-dilute suspension of squirmers can be found in Ishikawa and Pedley (2007a), based on the Stokesian-dynamics method (cf Brady and Bossis, 1988). In the absence of Brownian motion and at negligible particle Reynolds number, the equation of motion for A^ identical squirmers suspended in a Newtonian solvent fluid otherwise at rest can be written as; -R.U + F,,+F,„,+F,,^=0. (3) Here U consists of the translational-rotational velocities of the A^ particles evaluated at the squirmer centre. R is the grand resistance matrix, which is constructed by a pairwise superposition of exact two inert sphere results. The pairwise additivity is an approximation, but it is expected to be justi-fied if the particle volume fraction is not too large (defining semi-dilute). ¥sq is the force-torque due to the squirming motion, which is calculated from superposition of pairwise interaction between squirmers, ^tor is the external torques due to the bottom-heaviness. F^^/? is the non-hydrodynami

 interparticle forces introduced in order to avoid the prohibitively small time step needed to overcome the problem of overlapping particles. To model a suspension of infinite extent, periodic boundary conditions were employed