standard methods for study of operator inequalities (such as majorization
theory and so on) are summarized at the end of each chapter together with
suitable references, which might be of some help to the reader.
In the rest we will explain historical background at first and then more
details on the contents of the present monograph. In the classical work [36]
E. Heinz showed the (operator) norm inequalityfor positive operators H, K ≥ 0 and an arbitrary operator X on a Hilbert
space. In the 1979 article [64] A. McIntosh presented a simple proof ofwhich is obviously equivalent to the following estimate for positive operators:It is the special case θ = 1/2 of (1.3), and he pointed out that a simple and
unified approach to so-called Heinz-type inequalities such as (1.3) (and the
“difference version” (8.7)) is possible based on this arithmetic-geometric mean
inequality. The closely related eigenvalue estimatefor positive matrices is known ([12]). Here, {µn(·)}n=1,2,··· denotes singular
numbers, i.e., µn(Y ) is the n-th largest eigenvalue (with multiplicities counted)
of the positive part |Y | = (Y ∗Y )1/2. This means |H1/2K1/2| ≤ 1
2U(H +K)U∗
for some unitary matrix U so that we havefor matrices, which of course remains valid for Hilbert space operators H, K ≥
0 and X by the standard approximation argument. On the other hand, in [3]
T. Ando obtained the matrix Young inequalityfor p, q > 1 with p−1 + q−1 = 1. Although the weak matrix Young inequality

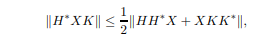
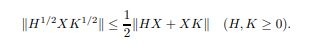



No comments:
Post a Comment